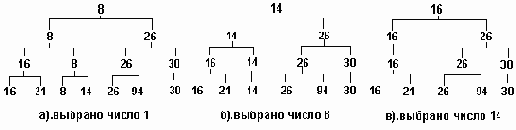
Пирамида после последовательных выборок

Рисунок3.14. Пирамида после последовательных выборок

Процедура Heap_Sort получает входной параметр ph - указатель на вершину пирамиды. и формирует выходной параметр a - упорядоченный массив чисел. Вся процедура Heap_Sort состоит из цикла, в каждой итерации которого значение из вершины переносится в массив a, а затем вызывается функция Competit, которая обеспечивает реорганизацию пирамиды в связи с удалением значения из вершины.

Функция Competet рекурсивная, ее параметром является указатель на вершину того поддерева, которое подлежит реорганизации. В первой фазе функции устанавливается, есть ли у узла, составляющего вершину заданного поддерева, потомок, значение данных в котором совпадает со значением данных в вершине. Если такой потомок есть, то функция Competit вызывает сама себя для реорганизации того поддерева, вершиной которого является обнаруженный потомок. После реорганизации адрес потомка в узле заменяется тем адресом, который вернул рекурсивный вызов Competit. Если после реорганизации оказывается, что у узла нет потомков (или он не имел потомков с самого начала), то узел уничтожается и функция возвращает пустой указатель. Если же у узла еще остаются потомки, то в поле данных узла заносится значение данных из того потомка, в котором это значение наименьшее, и функция возвращает прежний адрес узла.

{===== Программный пример 3.12 =====} { Турнирная сортировка } type nptr = ^node; { указатель на узел } node = record { узел дерева } key : integer; { данные } left, right : nptr; { указатели на потомков } next : nptr; { указатель на "брата" } end; { Создание дерева - функция возвращает указатель на вершину созданного дерева } Function Heap_Create(a : Seq) : nptr; var i : integer; ph2 : nptr; { адрес начала списка уровня } p1 : nptr; { адрес нового элемента } p2 : nptr; { адрес предыдущего элемента } pp1, pp2 : nptr; { адреса соревнующейся пары } begin { Фаза 1 - построение самого нижнего уровня пирамиды } ph2:=nil; for i:=1 to n do begin New(p1); { выделение памяти для нового эл-та } p1^.key:=a[i]; { запись данных из массива } p1^.left:=nil; p1^.right:=nil; { потомков нет } { связывание в линейный список по уровню } if ph2=nil then ph2:=p1 else p2^.next:=p1; p2:=p1; end; { for } p1^.next:=nil; { Фаза 2 - построение других уровней } while ph2^.next<>nil do begin { цикл до вершины пирамиды } pp1:=ph2; ph2:=nil; { начало нового уровня } while pp1<>nil do begin { цикл по очередному уровню } pp2:=pp1^.next; New(p1); { адреса потомков из предыдущего уровня } p1^.left:=pp1; p1^.right:=pp2; p1^.next:=nil; { связывание в линейный список по уровню } if ph2=nil then ph2:=p1 else p2^.next:=p1; p2:=p1; { состязание данных за выход на уровень } if (pp2=nil)or(pp2^.key > pp1^.key) then p1^.key:=pp1^.key else p1^.key:=pp2^.key; { переход к следующей паре } if pp2<>nil then pp1:=pp2^.next else pp1:=nil; end; { while pp1<>nil } end; { while ph2^.next<>nil } Heap_Create:=ph2; end; { Реорганизация поддерева - функция возвращает указатель на вершину реорганизованного дерева } Function Competit(ph : nptr) : nptr; begin { определение наличия потомков, выбор потомка для реорганизации, реорганизация его } if (ph^.left<>nil)and(ph^.left^.key=ph^.key) then ph^.left:=Competit(ph^.left) else if (ph^.right<>nil) then ph^.right:=Competit(ph^.right); if (ph^.left=nil)and(ph^.right=nil) then begin { освобождение пустого узла } Dispose(ph); ph:=nil; end; else { состязание данных потомков } if (ph^.left=nil) or ((ph^.right<>nil)and(ph^.left^.key > ph^.right^.key)) then ph^.key:=ph^.right^.key else ph^.key:=ph^.left^.key; Competit:=ph; end; { Сортировка } Procedure Heap_Sort(var a : Seq); var ph : nptr; { адрес вершины дерева } i : integer; begin ph:=Heap_Create(a); { создание дерева } { выборка из дерева } for i:=1 to N do begin { перенос данных из вершины в массив } a[i]:=ph^.key; { реорганизация дерева } ph:=Competit(ph); end; end;

Построение дерева требует N-1 сравнений, выборка - N*log2(N) сравнений. Порядок алгоритма, таким образом, O(N*log2(N)). Сложность операций над связными структурами данных, однако, значительно выше, чем над статическими структурами. Кроме того, алгоритм неэкономичен в отношении памяти: дублирование данных на разных уровнях пирамиды приводит к тому, что рабочая область памяти содержит примерно 2*N узлов.